т р е н а ж ё р
ЕГЭ 2024. №8(7)
Касательная и производная.
Исследование функции.
Интерактивные тренажёры от
Лейсан Ахсановны Фахрутдиновой
Лейсан Ахсановны Фахрутдиновой

СКОРОСТЬ
материальной точки
в момент времени t:
v(t) = xʹ(t)
материальной точки
в момент времени t:
v(t) = xʹ(t)
x(t) - закон движения материальной точки
1 шаг
x(t) - закон движения материальной точки
Находим производную:
xʹ(t) = 12t - 48 = v(t);
xʹ(t) = 12t - 48 = v(t);
2 шаг
По условию задачи t = 9с:
v(t) = 12t - 48 = 12•9 - 48 = 60 м/с
ОТВЕТ: 60
v(t) = 12t - 48 = 12•9 - 48 = 60 м/с
ОТВЕТ: 60
1 шаг
x(t) - закон движения материальной точки
Находим производную:
v(t) = xʹ(t) = 2t - 13;
v(t) = xʹ(t) = 2t - 13;
2 шаг
По условию задачи v(t) = 3 м/с:
2t - 13 = 3;
t = 8 c.
ОТВЕТ: 8
2t - 13 = 3;
t = 8 c.
ОТВЕТ: 8
1 тип:
исследуем график функции f(x)
(промежутки возрастания и убывания)
исследуем график функции f(x)
(промежутки возрастания и убывания)
2 тип:
исследуем график производной функции fʹ(x)
(промежутки положительных и отрицательных значений производной)
исследуем график производной функции fʹ(x)
(промежутки положительных и отрицательных значений производной)
Задачи делим на два типа:
Задачи на исследование решаем через составление схемы
1 шаг
проводим координатную ось ОХ
2 шаг
слева, над осью, подписываем производную - fʹ(x);
слева, под осью, подписываем функцию - f(x)
слева, под осью, подписываем функцию - f(x)
fʹ(x)
f(x)
3 шаг
из графика выписываем абсциссы точек (х1, х2,...)
х1
х2
х3
хn
4 шаг
над осью проставляем ЗНАКИ ПРОИЗВОДНОЙ:
"+" - над промежутком, где производная принимает положительное значение;
"-" - над промежутком, где производная принимает отрицательное значение
(на данном рисунке знаки выставлены только для примера)
"+" - над промежутком, где производная принимает положительное значение;
"-" - над промежутком, где производная принимает отрицательное значение
(на данном рисунке знаки выставлены только для примера)
+
-
+
5 шаг
под осью расставляем стрелки для ФУНКЦИИ:
↑ - в этом промежутке функция ВОЗРАСТАЕТ - СТРОГО под знаком "+";
↓ - в этом промежутке функция УБЫВАЕТ - СТРОГО под знаком "-"
↑ - в этом промежутке функция ВОЗРАСТАЕТ - СТРОГО под знаком "+";
↓ - в этом промежутке функция УБЫВАЕТ - СТРОГО под знаком "-"
↑
↑
↑
6 шаг
по схеме отвечаем на вопросы задачи
х
Чтение схемы
1) точки экстремума - х2, х3
х2 - точка максимума функции;
х3 - точка минимума функции
х2 - точка максимума функции;
х3 - точка минимума функции
fʹ(x)
f(x)
х1
х2
х3
хn
+
-
+
↑
↑
↑
х

2) в точках экстремума fʹ(x) = 0
fʹ(x)
f(x)
-6
+
-
+
↑
х
Задача 6.1.
1 шаг
2 шаг
3 шаг
4 шаг
5 шаг
6 шаг
На графике - ФУНКЦИЯ.
ЗНАЧИТ - выделяем промежутки возрастания и убывания
ЗНАЧИТ - выделяем промежутки возрастания и убывания
переносим значения на ось Х
-3
5,6
7
-3
0
5,6
7
8
расставляем стрелки возрастания и убывания
↑
↑
↑
↑
↑
↑
↑
↑
↑
по стрелкам определяем ЗНАК ПРОИЗВОДНОЙ и записываем над осью Х
-
-
выделяем промежутки, где ПРОИЗВОДНАЯ ПОЛОЖИТЕЛЬНА
СЧИТАЕМ количество целых точек(целые числа):
-2, -1, 6 - всего ТРИ точки. ОТВЕТ: 3
-2, -1, 6 - всего ТРИ точки. ОТВЕТ: 3
ПОМНИМ! В точках, где меняются знаки - производная равна нулю.
6
-2
-1
7 шаг
fʹ(x)
f(x)
+
х
Задача 6.2.
1 шаг
2 шаг
3 шаг
4 шаг
5 шаг
На графике - ФУНКЦИЯ.
ЗНАЧИТ - выделяем промежутки возрастания и убывания
ЗНАЧИТ - выделяем промежутки возрастания и убывания
переносим значения на ось Х
1
расставляем стрелки возрастания и убывания
↑
↑
↑
↑
↑
↑
по стрелкам определяем ЗНАК ПРОИЗВОДНОЙ и записываем над осью Х
-
выписываем точки ЭКСТРЕМУМА
(точки максимума и точки минимума):
1, 2, 4, 7, 9, 10, 11
Считаем их сумму:
1 + 2 + 4 + 7 + 9 + 10 + 11 = 44
ОТВЕТ: 44
(точки максимума и точки минимума):
1, 2, 4, 7, 9, 10, 11
Считаем их сумму:
1 + 2 + 4 + 7 + 9 + 10 + 11 = 44
ОТВЕТ: 44
7
2
4
9
10
11
-2
2
4
7
9
10
11
12
↑
↑
↑
↑
↑
↑
↑
↑
↑
↑
+
+
+
-
-
-
fʹ(x)
f(x)
-
+
х
Задача 6.3.
1 шаг
2 шаг
3 шаг
4 шаг
5 шаг
На графике - ПРОИЗВОДНАЯ.
ЗНАЧИТ - выделяем промежутки знаков производной:
"+" - график выше оси ОХ;
"-" - график ниже оси ОХ
ЗНАЧИТ - выделяем промежутки знаков производной:
"+" - график выше оси ОХ;
"-" - график ниже оси ОХ
переносим значения и знаки на ось Х
-3
смотрим на знаки и расставляем стрелки возрастания и убывания
↑
↑
выделяем отрезок [-3;2], конечные точки включены.
-
-3
+
-8
3
-
обращаем внимание, как ведёт себя стрелка под этим отрезком:
она направлена ВНИЗ от точки (-3) к точке (2)
ЗНАЧИТ, (-3) расположена выше на этом отрезке и в этой точке ФУНКЦИЯ принимает наибольшее значение.
ОТВЕТ:-3
она направлена ВНИЗ от точки (-3) к точке (2)
ЗНАЧИТ, (-3) расположена выше на этом отрезке и в этой точке ФУНКЦИЯ принимает наибольшее значение.
ОТВЕТ:-3
↑
2
fʹ(x)
f(x)
-
+
х
Задача 6.4.
1 шаг
2 шаг
3 шаг
4 шаг
5 шаг
На графике - ПРОИЗВОДНАЯ.
ЗНАЧИТ - выделяем промежутки знаков производной:
"+" - график выше оси ОХ;
"-" - график ниже оси ОХ
ЗНАЧИТ - выделяем промежутки знаков производной:
"+" - график выше оси ОХ;
"-" - график ниже оси ОХ
переносим значения и знаки на ось Х
7
смотрим на знаки и расставляем стрелки возрастания и убывания
↑
↑
выделяем отрезок [-6;9], конечные точки включены.
-
7
+
-7
12
-
на данном отрезке только одна точка максимума
ОТВЕТ: 1
ОТВЕТ: 1
10
+
-
14
+
10
12
-
↑
↑

fʹ(x)
f(x)
+
х
Задача 6.5.
1 шаг
2 шаг
3 шаг
4 шаг
5 шаг
На графике - ФУНКЦИЯ.
ЗНАЧИТ - выделяем промежутки возрастания и убывания
ЗНАЧИТ - выделяем промежутки возрастания и убывания
переносим значения на ось Х
-2
расставляем стрелки возрастания и убывания
↑
↑
↑
↑
по стрелкам определяем ЗНАК ПРОИЗВОДНОЙ и записываем над осью Х
-
производная равна нулю в точках, где меняется знак (в точках экстремума)
Количество таких точек: 5
ОТВЕТ: 5
Количество таких точек: 5
ОТВЕТ: 5
1
-2
-1
4
6
-3
-1
1
4
6
9
↑
↑
↑
↑
↑
↑
↑
↑
+
+
-
-
+
Задача 6.6.
1 шаг
2 шаг
3 шаг
4 шаг
На графике - ФУНКЦИЯ.
Производная положительна на промежутках, где функция возрастает
(↑+)
Производная положительна на промежутках, где функция возрастает
(↑+)
расставляем стрелки возрастания и знак "+"
↑
↑
выделяем точки из задания, которые попали в промежутки возрастания
считаем полученные точки
Количество таких точек: 5
ОТВЕТ: 5
Количество таких точек: 5
ОТВЕТ: 5
↑
↑
↑
+
+
+
+
+
Задача 6.7.
1 шаг
2 шаг
3 шаг
4 шаг
На графике - ПРОИЗВОДНАЯ.
Функция возрастает там, где производная принимает положительное значение (↑+)
Функция возрастает там, где производная принимает положительное значение (↑+)
расставляем знаки "+" и стрелки возрастания ↑
↑
выделяем точки из задания, которые попали в промежутки возрастания
считаем полученные точки
Количество таких точек: 3
ОТВЕТ: 3
Количество таких точек: 3
ОТВЕТ: 3
↑
+
Касательная и окружность
касательная и секущая → прямая → y=kx+b
касательная
секущая
Прямая на координатной плоскости
прямая направлена вверх при k>0
угол - острый
угол - острый

y = kx + b
x
y
прямая направлена вниз при k<0
угол - тупой
угол - тупой

y = kx + b
x
y
прямая параллельна оси ОХ при k=0
нет угла
нет угла
y = kx + b
x
y
Условие параллельности прямых
прямые параллельны при k1 = k2
y = k1x + b
x
y
y = k2x + b
Условие перпендикулярности прямых
прямые перпендикулярны при k1 • k2 = -1
y = k1x + b
x
y
y = k2x + b
Угловой коэффициент - k

k = tgα = (y1/x1) > 0
угол - острый
угол - острый
y = kx + b
(k>0)
(k>0)
x
y
y1
x1
α

k = - tgα = - (y1/x1) < 0
угол - тупой
угол - тупой
y = kx + b
(k<0)
(k<0)
x
y
y1
x1
α
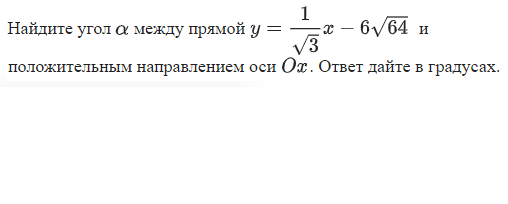
Задача 2.1. Нахождение угла между прямой и осью
1 шаг
2 шаг
3 шаг
4 шаг
анализируем данные:
прямая y = -5x - 6 параллельна касательной y = kx + b, значит k = -5;
НАЙТИ: х0
точка касания х0 только в формуле fʹ(x0) = k, значит, работаем по этой формуле
НАЙТИ: х0
точка касания х0 только в формуле fʹ(x0) = k, значит, работаем по этой формуле
записываем формулу производной в точке касания:
fʹ(x0) = k
вычисляем производную в точке касания:
fʹ(x0) = (х02 + 8х0 - 7)ʹ = 2х0 + 8
подставляем найденные значения в формулу (2 шаг):
fʹ(x0) = k
2х0 + 8 = -5;
х0 = -6,5 - ответ
2х0 + 8 = -5;
х0 = -6,5 - ответ
РЕШЕНИЕ:
k = 1/√3, k>0, угол - острый
tgα = k = 1/√3
tgα = k = 1/√3
tgα = 1/√3;
α = π/6
α = 300
α = π/6
α = 300
Ответ: 300
КАСАТЕЛЬНАЯ к графику функции y=f(x)

y = f(x)
x
y
Значение производной в точке касания х0

y = f(x)
x
y

f′(x0) = k = tgα (при k>0, острый угол)
f′(x0) = k = -tgα (при k<0, тупой угол)
f′(x0) = k = -tgα (при k<0, тупой угол)
x0
α
y = kx + b (k>0)
ВЫУЧИТЬ!
f′(x0) = k
f′(x0) = k
x0 - абсцисса точки касания

y = f(x)
x
y
f′(x0) = k = 0
(касательная параллельна оси ОХ)
(касательная параллельна оси ОХ)
y = b (k=0)
y = b (k=0)
x0
x0
ВЫУЧИТЬ!
f′(x0) = k
f′(x0) = k
x0 - абсцисса точки касания
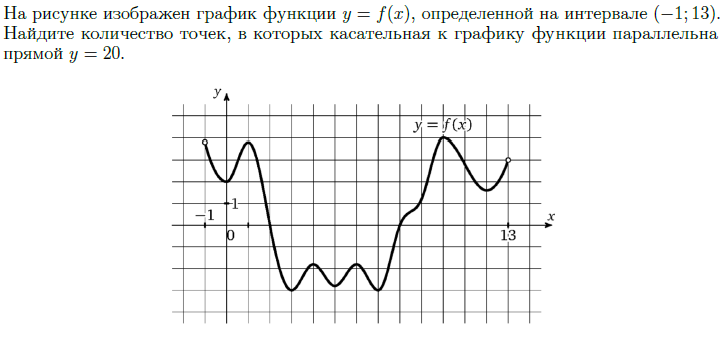
Задача 3.2
(решите и проверьте ответ)





ПРОВЕРИТЬ
у=20




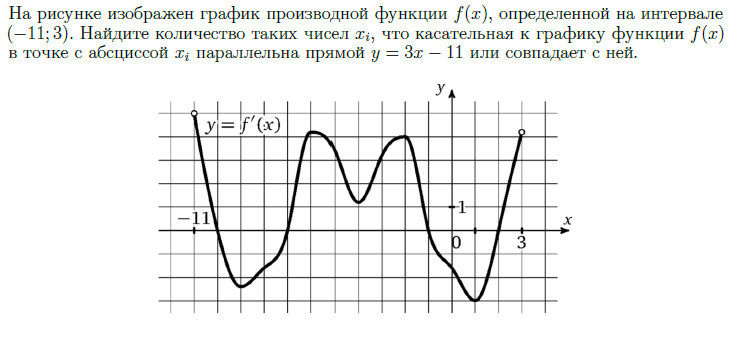
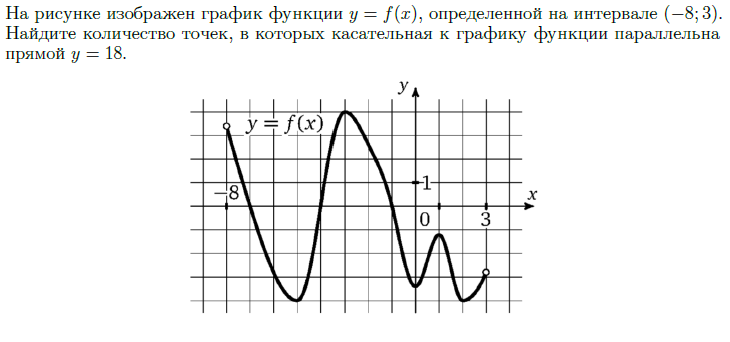
Задача 3.3
1 шаг
Касательная у=кх + b
параллельна прямой
у=3х - 11, значит,
k1=k2=3.
Знаем, что производная f'(x) = k.
Нам нужно определить количество точек, в которых производная равна 3.
Проводим прямую у=3
параллельна прямой
у=3х - 11, значит,
k1=k2=3.
Знаем, что производная f'(x) = k.
Нам нужно определить количество точек, в которых производная равна 3.
Проводим прямую у=3
(для просмотра РЕШЕНИЯ нажимайте на ШАГ)
2 шаг
3 шаг
считаем количество точек пересечения





Ответ: 6
у=3



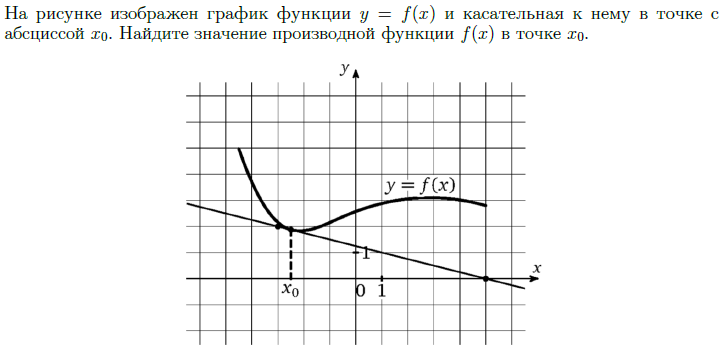
Задача 3.5. Значение производной в точке касания.
1 шаг
выделяем точки, которые указаны на чертеже
(для просмотра РЕШЕНИЯ нажимайте на ШАГ)
2 шаг
3 шаг
строим третью точку так, чтобы получился прямоугольный треугольник
(гипотенуза ВСЕГДА лежит на касательной)
(гипотенуза ВСЕГДА лежит на касательной)
ВЫУЧИТЬ!
f′(x0) = k = tg α
f′(x0) = k = tg α



проводим расчёт по формуле
у1 - 2 клетки, х1 - 8 клеток
fʹ(x0) = k = -tgα = -(y1/x1) = -(2/8) = -0,25
у1 - 2 клетки, х1 - 8 клеток
fʹ(x0) = k = -tgα = -(y1/x1) = -(2/8) = -0,25
4 шаг
-определяем угол между касательной и осью ОХ;
-так как прямая направлена вниз, то к<0, значит - угол тупой
ответ со знаком "-".
-так как прямая направлена вниз, то к<0, значит - угол тупой
ответ со знаком "-".

x0 - абсцисса точки касания
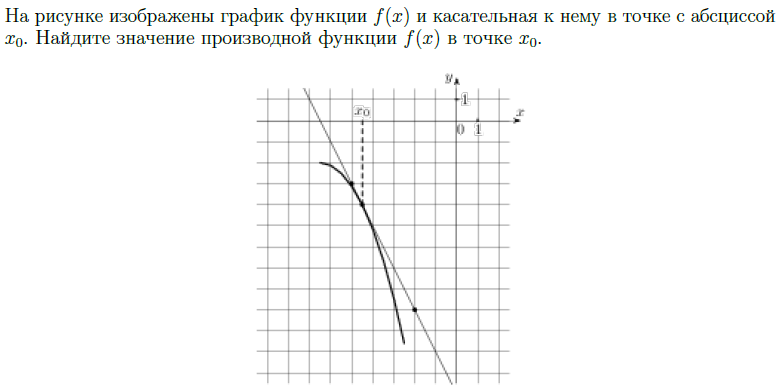
Задача 3.6. Значение производной в точке касания.
(решите самостоятельно и ПРОВЕРЬТЕ результат)
ВЫУЧИТЬ!
f′(x0) = k = tg α
f′(x0) = k = tg α



проводим расчёт по формуле:
красная прямая - касательная;
чёрная прямая - параллельный перенос оси ОХ;
угол - тупой;
у1 - 6 клеток, х1 - 3 клетки;
fʹ(x0) = k = -tgα = -(y1/x1) = -(6/3) = -2
красная прямая - касательная;
чёрная прямая - параллельный перенос оси ОХ;
угол - тупой;
у1 - 6 клеток, х1 - 3 клетки;
fʹ(x0) = k = -tgα = -(y1/x1) = -(6/3) = -2
ПРОВЕРИТЬ

x0 - абсцисса точки касания
НАИБОЛЬШЕЕ значение производной в точке касания х0
y = f(x)
x
y

Если угол ОСТРЫЙ, то в точке х0 производная достигает НАИБОЛЬШЕГО значения.
(при k > 0 - наибольшее значение производной в точке х0)
(при k > 0 - наибольшее значение производной в точке х0)
x0
α
y = kx + b (k>0)
f′(x0) > 0
x0 - абсцисса точки касания
НАИМЕНЬШЕЕ значение производной в точке касания х0
y = f(x)
x
y

Если угол ТУПОЙ, то в точке х0 производная достигает НАИМЕНЬШЕГО значения.
(при k < 0 - наименьшее значение производной в точке х0)
(при k < 0 - наименьшее значение производной в точке х0)
x0
y = kx + b (k<0)
f′(x0) < 0
x0 - абсцисса точки касания
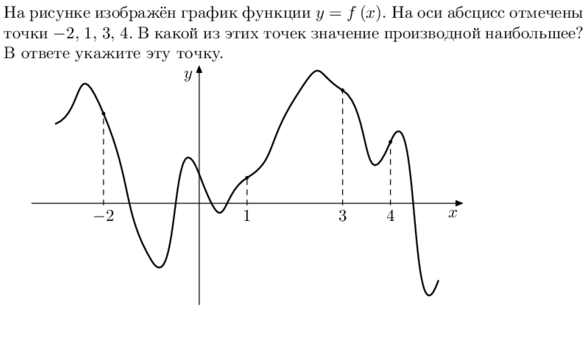

Задача 4.1. Наибольшее значение производной.
1 шаг
находим острые углы
(наибольшее значение при k>0)
(наибольшее значение при k>0)
(решите самостоятельно и ПРОВЕРЬТЕ результат)
2 шаг
3 шаг
из двух острых углов выбираем наибольший (визуально, это угол при х=4)
ОТВЕТ: 4
ОТВЕТ: 4

проводим касательные в указанных точках касания

(для просмотра РЕШЕНИЯ нажимайте на ШАГ)
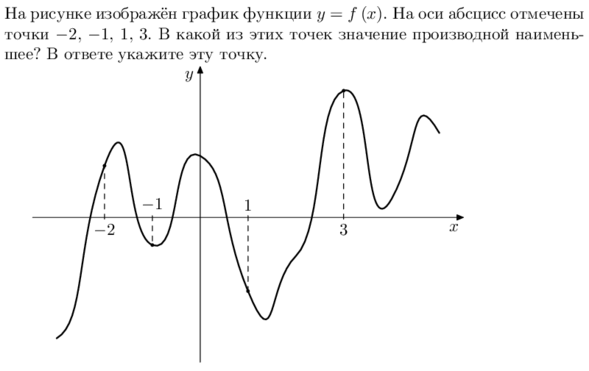

Задача 4.2. Наименьшее значение производной.
1 шаг
находим тупые углы
(наименьшее значение при k<0)
(наименьшее значение при k<0)
(решите самостоятельно и ПРОВЕРЬТЕ результат)
2 шаг
3 шаг
из двух тупых углов выбираем самый маленький (визуально, это угол при х=1);
в этой точке производная принимает наименьшее значение.
ОТВЕТ: 1
в этой точке производная принимает наименьшее значение.
ОТВЕТ: 1

проводим касательные в указанных точках касания

(для просмотра РЕШЕНИЯ нажимайте на ШАГ)

Задача 3.6 . Нахождение абсциссы точки касания.
1 шаг
2 шаг
3 шаг
4 шаг
анализируем данные:
прямая y = -5x - 6 параллельна касательной y = kx + b, значит k = -5;
НАЙТИ: х0
точка касания х0 только в формуле fʹ(x0) = k, значит, работаем по этой формуле
НАЙТИ: х0
точка касания х0 только в формуле fʹ(x0) = k, значит, работаем по этой формуле
записываем формулу производной в точке касания:
fʹ(x0) = k
вычисляем производную в точке касания:
fʹ(x0) = (х02 + 8х0 - 7)ʹ = 2х0 + 8
подставляем найденные значения в формулу (2 шаг):
fʹ(x0) = k
2х0 + 8 = -5;
х0 = -6,5 - ответ
2х0 + 8 = -5;
х0 = -6,5 - ответ

Задача 3.7 . Нахождение абсциссы точки касания.
ПРОВЕРИТЬ:
k = 8
fʹ(x0) = k
fʹ(x0) = k
fʹ(x0) = (х02 - 3х0 + 8)ʹ = 2х0 - 3
2х0 - 3 = 8;
х0 = 5,5 - ответ
х0 = 5,5 - ответ
(решите самостоятельно и ПРОВЕРЬТЕ результат)

Задача 3.8 . Нахождение абсциссы точки касания.
(если получились два х0)
(если получились два х0)
5 шаг
4 шаг
После выполнения 1 шаг - 4 шаг из Задачи 6 получили две точки касания. Какую выбрать?
Подставляем каждую точку х0 в формулы прямой и функции. Там, где значения y совпадут, ту точку х0 и выписываем в ответ:
при х0 = 0:
у = -х + 4 = 0 + 4 = 4
у = х3 + х2 - х + 4 = 4
значения у совпали
у = -х + 4 = 0 + 4 = 4
у = х3 + х2 - х + 4 = 4
значения у совпали
ОТВЕТ: 0
fʹ(x0) = k
3х02 + 2х0 - 1= -1;
3х02 + 2х0 = 0;
х0 = 0 или х0 = - (2/3)
3х02 + 2х0 - 1= -1;
3х02 + 2х0 = 0;
х0 = 0 или х0 = - (2/3)
при х0 = - (2/3):
у = -х + 4 = 10/3 = 90/27
у = х3 + х2 - х + 4 = 130/27
значения у разные
у = -х + 4 = 10/3 = 90/27
у = х3 + х2 - х + 4 = 130/27
значения у разные

Задача 5.1 . Нахождение коэффициента a (b, с).
1 шаг
2 шаг
3 шаг
Прямая является касательной, значит, используем формулу
k = 3,
k = 3,
Подставляем в функцию у = ах02 + 2х0 + 3 найденное значение а, получаем:
fʹ(x0) = k :
fʹ(x0) = (ax02 + 2x0 + 3)ʹ = 2ax0 + 2;
2ах0 + 2 = 3;
а = 1 / (2х0)
2ах0 + 2 = 3;
а = 1 / (2х0)
; х0 = 4
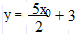
Так как касательная и функция имеют общую точку, то приравняем правые части формул и найдём значение х0:
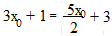
4 шаг
возвращаемся в 1 шаг и находим а:
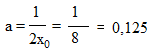
Исследование функции
Выполнить тестирование ТОЛЬКО после прохождения обучения
| начать тест |
Какой угол между прямой и осью ОХ?

| следующий вопрос |
| проверить |
| результат |
Какой угол образует прямая у = -7х + 6 с осью ОХ?
| следующий вопрос |
| проверить |
| результат |
Какая из указанных прямых является касательной?

| следующий вопрос |
| проверить |
| результат |
Прямые перпендикулярны при...
| следующий вопрос |
| проверить |
| результат |
В какой точке производная принимает наибольшее значение?

| следующий вопрос |
| проверить |
| результат |
Если дан график ФУНКЦИИ, то исследование начинаем ...
| следующий вопрос |
| проверить |
| результат |
Какой угол образуется между прямой и осью ОХ?

| следующий вопрос |
| проверить |
| результат |
В какой точке производная принимает наименьшее значение?

| следующий вопрос |
| проверить |
| результат |
Прямые параллельны при...
| следующий вопрос |
| проверить |
| результат |
Точки экстремума - это ...
| следующий вопрос |
| проверить |
| результат |
Скорость материальной точки равен ...
| следующий вопрос |
| проверить |
| результат |
Какой угол образует прямая у = -8 с осью ОХ?
| следующий вопрос |
| проверить |
| результат |
Какая прямая является секущей?

| следующий вопрос |
| проверить |
| результат |
Производная функции в точке х0 касания равна...
| следующий вопрос |
| проверить |
| результат |
Повторите обучение!
| повторить тест |
Практически получилось, но надо ещё повторить правила!
| повторить тест |
Вы успешно прошли обучение!
| повторить тест |
Поддержать проект
Ваши впечатления от проекта
Находясь на сайте, вы даёте согласие на использование файлов cookie
OK